Page 1 of 1
Exponential Problem with Natural Consolidation
Posted: Wed May 22, 2013 4:40 am
by conray
Whats wrong with TM1 displaying values like (0,000000000000)?
I have a natural consolidation [CD Amt], calculated using [Std Amt] - [Act Amt].
By calculating it manually, i get a value of 0.
But the natural consolidation gives a (0,0000000000) value as shown in the attachment.
I have checked that there is no rounding issues and the values added up indeed is 0.
May i know what else could be the problem here?
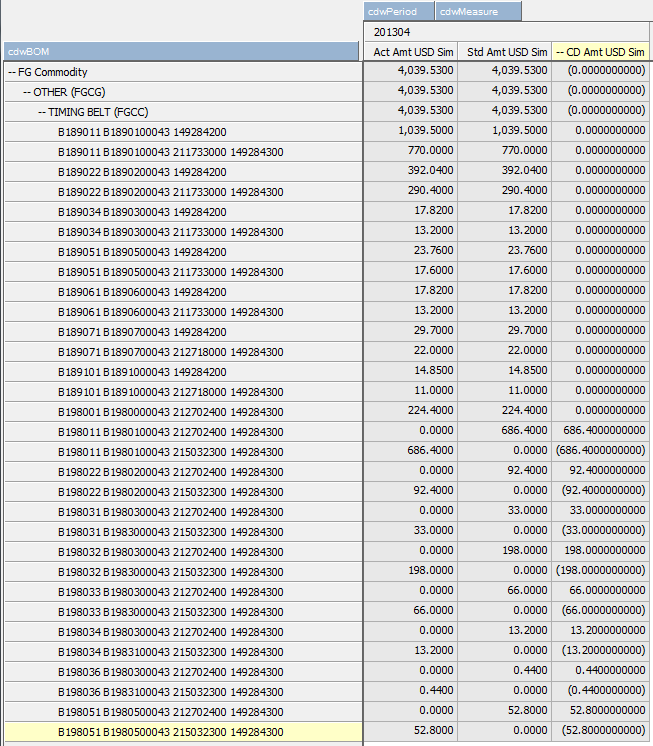
- Cubeview screenshot
- Natural Consolidation with exponential.gif (44.02 KiB) Viewed 19816 times
Re: Exponential Problem with Natural Consolidation
Posted: Wed May 22, 2013 5:52 am
by ioscat
Re: Exponential Problem with Natural Consolidation
Posted: Wed May 22, 2013 6:36 am
by cgaunt
Whilst I agree with Isocat that zero is not always zero, you should be able to control this affect in the formatting properties for the element in question.
Re: Exponential Problem with Natural Consolidation
Posted: Wed May 22, 2013 7:57 am
by ioscat
And you should be very careful in using this non-zero values
Re: Exponential Problem with Natural Consolidation
Posted: Wed May 22, 2013 9:34 am
by Duncan P
For those that don't have access to the IBM APAR system the link ioscat includes has this to say
Calculations may result in a very small number, but not zero. If this value is used as the denominator with the 'save divide' operator "\", the division will be done resulting in a very large number, instead of treating the very small calculated number as zero.
An example of this is when you calculate the reciprocal of one minus ten tenths :-
Code: Select all
1 \ ( 1 - ( 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 ) )
which gives 9007199254740900 and not 0.
Like ioscat said, you need to be careful.
Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 12:54 am
by rmackenzie
Duncan P wrote:An example of this is when you calculate the reciprocal of one minus ten tenths :-
Code: Select all
1 \ ( 1 - ( 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 ) )
which gives 9007199254740900 and not 0.
Duncan, that's interesting - if you substitute these rules then you get the correct answer of 0 per usage of 'safe divide':
Code: Select all
1 \ ( 1 - ( 0.25 + 0.25 + 0.25 + 0.25 ) );
Code: Select all
1 \ ( 1 - ( 0.2 + 0.2 + 0.2 + 0.2 + 0.2 ) );
Code: Select all
1 \ ( 1 - ( 0.125 + 0.125 + 0.125 + 0.125 + 0.125 + 0.125 + 0.125 + 0.125 ) );
But then try this which gives -4503599627370400:
Code: Select all
1 \ ( 1 - ( 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05 + 0.05) );
What's up with tenths and twentieths that works fine with halves, quarters, fifths and eighths? Looks like some sort of 'issue exists where denominator is 10 or greater' type of issue, perhaps?
This strikes me as a bug, wouldn't you agree? Plenty of customers that I've worked with think this problem should go away.
Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 4:18 am
by Andy Key
I would go for it being a limitation of IEEE-754 and the conversion of decimal to binary rather than a bug.
Do the same calculations (switching the \ to /) in Excel and you'll get the same results.
Now try doing the same with 64ths i.e. a number that can be represented in a precise manner in both decimal and binary (and is short enough to fit in to IEEE-754)
Code: Select all
1 \ ( 1 - ( 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 + 0.015625 ) )
in Excel you get a #Div/0! error and you get a full fat zero in TM1.
Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 6:28 am
by rmackenzie
Andy Key wrote:I would go for it being a limitation of IEEE-754 and the conversion of decimal to binary rather than a bug.
Do the same calculations (switching the \ to /) in Excel and you'll get the same results.
Seems to work ok on the calculator on the Windows desktop

Seriously, I've seen TM1 give some flakey rounding errors on standard consolidations. When the balance sheet stops balancing, it becomes a problem for people for whom an explanation involving IEEE-754 just doesn't cut it. On that point, I'm familiar with some of the issues in binary floating point arithmetic but are we saying that there's no solution, or advance, on a problem that's inherent to a standard dating back to, what, 1985??
Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 10:25 am
by Duncan P
The problem is that the only way to get the speed is to use a representation on which the standard arithmetic operations can be done in hardware. IEEE754-2008 defines a number of
decimal floating point representations but they are only supported in a small range of hardware (e.g. IBM Power6 and z9) and not on the standard Intel stuff. Hence we are stuck with the problems of rounding recurring binary representations of 1/5.
Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 11:06 am
by lotsaram
head_is_spinning

Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 11:10 am
by rmackenzie
Hey Duncan, thanks for the response - always welcome and appreciated. Just to play devil's advocate for a moment - wouldn't it be an interesting avenue to explore for TM1 to offer the same 'Precision as displayed' option that is referred to in this
Microsoft support note? That's kind of what the OP was referring to in the third post of the thread and not entirely worlds apart from the existing
SpreadingPrecision parameter available today in the tm1s.cfg ??
Re: Exponential Problem with Natural Consolidation
Posted: Thu May 23, 2013 11:11 am
by rmackenzie
lotsaram wrote:head_is_spinning

She'll be right

Re: Exponential Problem with Natural Consolidation
Posted: Tue Jun 04, 2013 7:36 am
by conray
So in summary, it is not possible to get a zero, unless using the "safe divide" method in the rule itself?
Re: Exponential Problem with Natural Consolidation
Posted: Thu Jun 06, 2013 8:55 am
by ioscat
Possibly yes and possibly no
Depends on
Re: Exponential Problem with Natural Consolidation
Posted: Wed Jun 12, 2013 4:40 am
by conray
ioscat wrote:Possibly yes and possibly no
Depends on
depends on what?
It really is annoying to get something like this with only 2 decimal point involve:
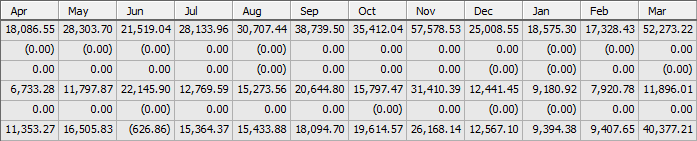
- Data
- ScreenHunter_04 Jun. 12 12.38.gif (10.96 KiB) Viewed 19552 times
look at all the (0.00)...
Re: Exponential Problem with Natural Consolidation
Posted: Wed Jun 12, 2013 8:00 am
by rmackenzie
conray wrote:So in summary, it is not possible to get a zero, unless using the "safe divide" method in the rule itself?
No, the safe divide is no guarantee of getting absolute zero. The summary of the problem is that human numbering system (decimal) and computer numbering system (binary) don't always place nicely. Sometimes there are extremely small rounding errors meaning that the zero value is actually an extremely small number. This leads to your zero suppression problem. Maybe what we need is some sort of config parameter like:
Re: Exponential Problem with Natural Consolidation
Posted: Mon Feb 23, 2015 5:41 pm
by Tilo
IBM states that this would be fixed in TM1 10.2 but it is not entirely if even or IBM means a Version above 10.2.0.
Create a formula as follows:
['a'] = N: ['b'];
where values for 'a' are entered directly and afterwards there is plain consolidation.
Then put 'a' and 'b' into a consolidation 'c'
where 'a' has the weight 1 and
b has the weight -1
then very often the result is c<>0 (e.g. 0,000000000000019387).
(at least in 10.2.0 and with our model).
This causes zero suppression Problems, calculation Problems (especially when using multiplication or backslash division, overfeeding
This does not happen (in our model) if you can create 'b' as consolidation of 'a' with the weight 1.
Re: Exponential Problem with Natural Consolidation
Posted: Sun Mar 01, 2015 11:46 am
by paulsimon
Hi
There is a TM1 Rule function ROUNDP
Won't that do what you need?
If all else fails use something like IF( ABS( [ cell ref ] ) < 0.0001 , 0 , [cell ref] )
Regards
Paul Simon
Re: Exponential Problem with Natural Consolidation
Posted: Mon Mar 02, 2015 1:29 pm
by tm1ist
When using a binary representation for numbers, it is expected to have very slight variations in numbers. It is because we use the decimal system and the binary system cannot represent all of the decimal numbers. It is vice versa, decimal numbers cannot represent some numbers in different bases as well. For instance, 1/3 is 0.33333333...33(which is never ending) in decimal system and when you multiply that 0.3333....33 with 3, you cannot get exactly 1. Long story short, as others explained, it is due to binary number system.
For financial applications, it is suggested to use decimal system because our monetary system is decimal and we don't have amounts like 1/3 USD which decimal system cannot represent. However, computer interpretation of decimal numbers takes longer time and memory, because the computer hardware works with 0 and 1(which is binary). This is not the case just for TM1 but also for any other software. In a programming language, when you compare the performance of a code piece when you use variable type double(which stores numbers as binary representation) or variable type decimal(stores as decimal representation), you will see that it will be faster when use variable type double. However, with double type you will have number precision issues like you do now with TM1. Also note that this precision issue is not just about 0 but for any number that is derived from some calculations of some noninteger values.
Therefore, what TM1 does is sacrificing monetary(base 10) number precision for faster performance. And, it gives you the chance to use a rounding function when you require the numbers to be exactly zero.
And the reason why 0.5, 0.25 etc can be represented in binary and 0.1, 0.2 cannot is about the exponents of 2. 2 exponent -1 is 1/2(0.5), 2 exponent -2 is 1/4(0.25) etc.